rm_balance/utils/Simulation-master/balance/series_legs/doc/2连杆分析.md

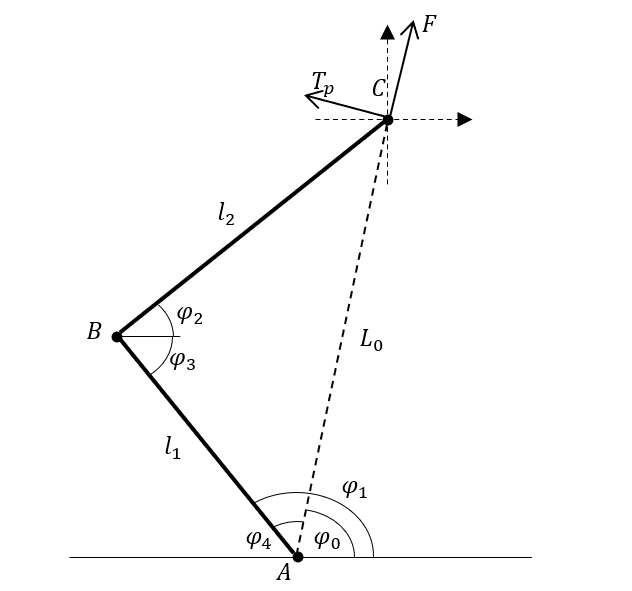
2连杆分析

参考：五连杆运动学解算与VMC

1 正运动学解算

$\phi_1$和$\phi_2$可由电机编码器测量得到。

$C$点坐标：

\left \{
    \begin{array}{l}
        x_C = l_1\cos\phi_1 + l_2\cos\phi_2\\
        y_C = l_1\sin\phi_1 + l_2\sin\phi_2
    \end{array}
\right .

得：

\left \{
    \begin{array}{l}
        L0 = \sqrt{x_C^2 + y_C^2} \\
        \phi_0 = \arctan{\frac{y_C}{x_C}}
    \end{array}
\right .

2 逆运动学解算

由余弦定理易得：

\phi_2+\phi_3 = \arccos\frac{l_1^2+l_2^2-L_0^2}{2l_1l_2}

又：

\phi_3 = \pi - \phi_1

得：

\phi_2 = \arccos\frac{l_1^2+l_2^2-L_0^2}{2l_1l_2}+\phi_1-\pi

3 雅可比矩阵

基于文中描述可得：

\left \{
    \begin{array}{l}
        \dot x_C = -l_1\dot\phi_1\sin\phi_1 - l_2\dot\phi_2\sin\phi_2\\
        \dot y_C = l_1\dot\phi_1\cos\phi_1 + l_2\dot\phi_2\cos\phi_2
    \end{array}
\right .

即：

\left [
    \begin{matrix}
        \dot x_C \\
        \dot y_C
    \end{matrix}
\right ]

 =
\left [
    \begin{matrix}
        -l_1\sin\phi_1 & -l_2\sin\phi_2 \\
         l_1\cos\phi_1 &  l_2\cos\phi_2
    \end{matrix}
\right ]

\left [
    \begin{matrix}
        \dot\phi_1 \\
        \dot\phi_2
    \end{matrix}
\right ]

记作：

\left [
    \begin{matrix}
        \dot x_C \\
        \dot y_C
    \end{matrix}
\right ]

 =
J_0

\left [
    \begin{matrix}
        \dot\phi_1 \\
        \dot\phi_2
    \end{matrix}
\right ]

下面操作与文中相同，可得：

J^T = J_0^TRM =
\left[
    \begin{matrix}
        l_1 \,\sin \left(\phi_0 -\phi_1 \right) & \frac{l_1 \,\cos \left(\phi_0 -\phi_1 \right)}{L_0 }\\
        l_2 \,\sin \left(\phi_0 -\phi_2 \right) & \frac{l_2 \,\cos \left(\phi_0 -\phi_2 \right)}{L_0 }
    \end{matrix}
\right]

即：

J =
\left[
    \begin{matrix}
        l_1 \,\sin \left(\phi_0 -\phi_1 \right) & l_2 \,\sin \left(\phi_0 -\phi_2 \right)\\
        \frac{l_1 \,\cos \left(\phi_0 -\phi_1 \right)}{L_0 } & \frac{l_2 \,\cos \left(\phi_0 -\phi_2 \right)}{L_0 }
    \end{matrix}
\right]